The Philosophy of Social Evolution Part 2: Relatedness and Altruism

How can we explain the evolution of altruism? In part 2 of this series, Jonathan Birch considers “Hamilton’s Rule”.

Haldane’s quip

In what circumstances might natural selection favour self-sacrifice? As legend has it, the best known answer to this question was first spoken in a London pub called the Orange Tree. One night in the 1950s, after “calculating on the back of an envelope for some minutes”, J.B.S. Haldane remarked to John Maynard Smith – at the time, one of his graduate students – that “he was prepared to lay down his life for eight cousins or two brothers”.

If the story is true (and Maynard Smith insisted it was, though this has been disputed over the years), Haldane had latched on to a deep insight about the evolution of altruism. He had seen that genetic relatives have an evolutionary incentive to help one another. He had also seen that the incentive comes in degrees, and that the size of the incentive depends on the closeness of the helper’s genetic relationship to the beneficiary.

Haldane may not have been the first to see these things (R. A. Fisher grasped the basic point two decades earlier), but he may have been the first to glimpse their potential explanatory power. In a 1955 article,¹ he illustrated these ideas with a vivid example:

Let us suppose that you carry a rare gene which affects your behaviour so that you jump into a river and save a child, but you have one chance in ten of being drowned, while I do not possess the gene, and stand on the bank and watch the child drown. If the child is your own child or your brother or sister, there is an even chance that the child will also have the gene, so five such genes will be saved in children for one lost in an adult. If you save a grandchild or nephew the advantage is only two and a half to one. If you only save a first cousin, the effect is very slight. If you try to save your first cousin once removed the population is more likely to lose this valuable gene than to gain it.

He went on, however, to suggest that this idea was probably more applicable to insects than to humans:

But on the two occasions when I have pulled possibly drowning people out of the water (at an infinitesimal risk to myself) I had no time to make such calculations. Palaeolithic men did not make them. It is clear that genes making for conduct of this kind would only have a chance of spreading in rather small populations where most of the children were fairly near relatives of the man who risked his life. It is not easy to see how, except in small populations, such genes could have been established. Of course the conditions are even better in a community such as a beehive or an ants’ nest, whose members are all literally brothers and sisters.

Although Haldane never captured these thoughts in a detailed model, we can see here the subtlety of his thinking. He saw a gene for altruism might spread if the benefits fell differentially on other bearers of the gene, but he also saw that a mechanism that relied on organisms consciously calculating degrees of kinship was implausible. His proposed solution was small populations or communities: if a population or community is so small that everyone is a close relative of everyone else, the benefits of altruism will tend to fall on genetically similar individuals without the need for conscious calculation.

Hamilton’s rule

The Orange Tree was demolished in the spring of 1963. In the aftermath of the demolition, the Beatles arrived for a photoshoot, and a shot of them leaping above the rubble of Haldane’s old haunt would be used as the cover for their 1963 EP, Twist and Shout. Elsewhere in London, a graduate student called Bill Hamilton was making leaps of his own on Haldane’s foundations. He was working on a manuscript called ‘The Genetical Evolution of Social Behaviour’ – a manuscript that would change the way we think about the evolution of altruism.²

Hamilton had arrived at a more general form of Haldane’s insight, and he had captured it in a detailed mathematical framework. Crucially, he showed that the general sort of process Haldane had described did not require “rare genes” or “rather small populations”. Fundamentally, what is required is that the benefits of altruistic behaviour fall on recipients more likely than average to possess the genes for altruism.

Hamilton realised that the evolution of altruism depends, in a surprisingly simple way, on the cost to the actor and the benefit to the recipient – measured in the currency of reproductive success, or expected number of offspring – and on the closeness of the genetic relationship between them. In short: if sufficiently large benefits fall on sufficiently related recipients to offset the cost to the altruist, altruism can evolve by natural selection.

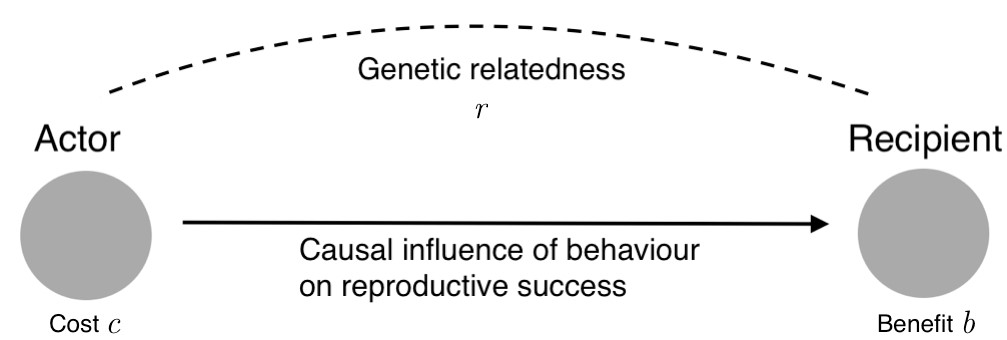
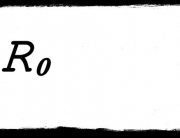
The precise mathematical relationship between cost, benefit and relatedness is captured in a principle now known as Hamilton’s rule. The rule states that a social behaviour will be favoured by natural selection if and only if rb > c, where “b” is the effect of the behaviour on the reproductive success of others, “c” is the effect on one’s own reproductive success, and “r” is the coefficient of relatedness, which measures the statistical association between the genes of the actor who performs the behaviour and the genes of the recipient affected by it.

The easiest way to understand the rationale behind the rule is to take a “gene’s eye” perspective. Imagine that you are a gene – what matters to you is the number of copies of yourself you leave in future generations. You have two ways to achieve this goal: a direct way and an indirect way. The direct way is to promote the reproductive success of the organism in which you are located. The indirect way is to promote the reproductive success of other organisms – provided those organisms are sufficiently likely to transmit copies of you to their offspring to make them worth the investment. Suppose a chance to help another organism arises. Should you help that organism or not? Hamilton’s rule can be thought of as capturing the cost-benefit calculation you have to make.

Having said that, I immediately want to row some of it back. The gene’s eye view makes Hamilton’s ideas easier to understand – as Richard Dawkins, one of Hamilton’s great champions over the years, is well aware. But gene’s eye thinking and inclusive fitness theory are not the same. Inclusive fitness theory involves taking an organism-level perspective, and estimating costs and benefits at the level of the organism. The goal is to explain the evolution of an organism-level trait (social behaviour) in terms of properties of interactions between organisms (costs, benefits and coefficients of relatedness) while recognising that these properties depend on the organisms’ genetic makeup. Thus inclusive fitness theory is, and always has been, an interesting hybrid of gene-level and organism-level thinking, and a proper interpretation of the theory needs to do justice to both its gene-centred and organism-centred aspects.

Hamilton’s rule: the genes for a social behaviour are selected if and only if rb > c, where b is the benefit conferred on a recipient, c is the cost imposed on the actor, and r is the coefficient of relatedness. (Figure from J. Birch, 2017, The Philosophy of Social Evolution, Oxford: Oxford University Press, © The Author.)

The rule under attack

Your initial reaction to Hamilton’s rule might well be: how can it be so simple? Aren’t the dynamics of natural selection messy and complicated? How can such a simple rule be anything more than an approximate rule of thumb, or perhaps a result that holds in certain special cases, given restrictive assumptions, but not in others? This is also the reaction of many mathematically trained biologists, and has been ever since Hamilton first derived the rule. A 2010 Nature article by Martin Nowak, Corina Tarnita and Edward O. Wilson kicked off a new round of debate on this issue – one that is still on-going.

Two chapters of The Philosophy of Social Evolution are devoted to this issue – far too little space to do justice to all of the objections thrown at Hamilton’s rule over the course of half a century. After studying this literature for some time, I’m fairly convinced that there is a version of Hamilton’s rule that is simple, exact, mathematically correct and surprisingly general. This is the version derived by David Queller in his 1992 paper “A General Model for Kin Selection“.

In this version, the famous “rb > c” form is still there, but the cost, benefit and relatedness coefficients have somewhat counterintuitive meanings. They are population statistics, calculated by averaging over all interacting pairs of organisms – not properties of “token” social interactions. These population statistics abstract away from messy detail to capture the overall statistical associations in a population between an organism’s genes, its own reproductive success, the genes of its social partners, and its social partners’ reproductive success.

People hear “cost” and “benefit” and think “payoffs” – but, except in very simple cases, cost and benefit are not payoff parameters but complicated functions of payoff parameters. Likewise, people hear “relatedness” and think “family trees” – but, except in very simple cases, relatedness cannot simply be read off from a family tree. It depends in complicated ways on the structure of the population. In short, r, b and c can depend in all kinds of ways on the population structure and the payoffs of social interaction, depending on the details of the case.

The precise way in which r, b and c depend on these parameters has consequences for how they change over time – and for what evolves over the long run. If rb > c now, the trait is being selected now – but what happens next depends on how r, b, c change as the population changes, and this can be very complicated indeed. Queller’s version of Hamilton’s rule thus provides a momentary snapshot, at a high level of abstraction, of underlying dynamics that are in fact every bit as messy and complicated as you would intuitively expect.

The organizing role of Hamilton’s rule

What’s the use of an abstract, high-level, statistical snapshot of a complex dynamical process? For some critics, this is a rhetorical question – the rule is simply useless. I disagree. I think snapshot principles of this type (other examples of which, by the way, include Price’s equation and Fisher’s “fundamental theorem”) are very useful for organizing our thinking about evolution. They are organizing frameworks, and Hamilton’s rule provides an organizing framework for the study of social evolution. It is no substitute for detailed modelling of evolutionary processes – but it is not intended to be. What it does is provide a framework in which we can tease out the common features of an apparently diverse class of models.

In particular, the rule tells us that any model in which true biological altruism (i.e. behaviour that detracts from the lifetime reproductive success of the actor and increases that of the recipient) evolves by natural selection must contain at least one source of positive “relatedness”, construed very broadly – that is, it must contain at least one source of positive genetic assortment between social partners. If you think you’ve made a model in which altruism evolves without positive genetic assortment, one of three things is going on:

the model implicitly contains a source of positive genetic assortment;
the behaviour is not altruistic in the sense of imposing a long-term cost on the actor (perhaps a short-term cost is offset by long-term gain, as in cases of “reciprocal altruism”);
an evolutionary process other than natural selection is driving the evolution of the trait.

What is ruled out by Hamilton’s rule is the evolution of altruism by natural selection without any positive genetic assortment at all. I know of no empirical examples that should lead us to rethink this result. What we find in amoebas, ants, bees, wasps, baboons, wolves and all kinds of other species is that the benefits of altruism are indeed directed differentially towards genetically related recipients. Humans are an interesting case, often proposed to be an exception – we’ll consider them in Part 5.

As Hamilton emphasized, there are many possible sources of positive genetic assortment, including kin recognition, group-mate recognition, shared habitat preference, limited dispersal from the group and more. What Hamilton’s rule allows us to see is that all such mechanisms enable the evolution of altruism for fundamentally the same reason – they all cause the benefits of altruism to be directed towards other bearers of the genes for altruism, making it possible that, in the right circumstances, rb might outweigh c.

In Part 3, I introduce an unusual, fascinating but poorly understood source of positive genetic assortment that arises in the world of microorganisms. That mechanism is horizontal gene transfer.

By Jonathan Birch

← Part 1Part 3 →

Jonathan Birch is Assistant Professor in the Department of Philosophy, Logic and Scientific Method, specializing in the philosophy of the biological sciences. Most of his work concerns the evolution of social behaviour. He is also interested in the evolution of morality, animal sentience, and the relation between sentience and welfare.