It’s often been thought that Curie’s principle says something that’s just obviously true about the world. However, Bryan Roberts has discovered a simple way in which Curie’s principle fails.
A matter of symmetry
Let’s start out by thinking about squares. We all know that squares are symmetrical but what exactly does this mean? Well, here’s a good way to think about it: when we say that a square is symmetrical we are saying that it will continue to look the same after we’ve done certain things to it. Draw a square on a piece of paper; rotate this drawing by 90 degrees and it will look indistinguishable from the original square in its original position. Rotate it by another 90 degrees and it still looks indistinguishable. Etc.
This property of the square is called invariance. When we say that our drawing looks the same after it has been rotated, we are saying that its shape doesn’t vary; that its shape is in-variant after having been rotated by 90 degrees.
Not only will it look the same after it has been rotated, our square will also look the same if we bisect it with a mirror and look at its reflection. As well as this, if we cut around our drawing and turn it over it will still look like a square. What this shows is that symmetry must be to do with more than just rotation.
What the rotation, the placing of the mirror and the turning-over have in common is that each one is an example of a way in which our square can be transformed. With this in mind we can give a nice general definition of what it is for something, anything, to be symmetrical: to be symmetrical is to be invariant under one or more given transformations.
Curie’s Principle
Although most of us think of symmetry as merely a property of shapes, symmetry is also a very important concept in fundamental physics.
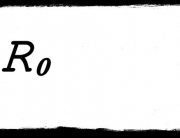
Something that has proved important for understanding the symmetries of the world is described by Curie’s Principle. Pierre Curie, husband of the perhaps-more-famous Marie, formulated his principle like this:
When certain effects show a certain asymmetry, this asymmetry must be found in the causes which gave rise to it.
What Curie’s Principle says is that whatever symmetry or asymmetry is present in an effect must also have been present in its cause, or, when it comes to symmetry, you don’t get out what hasn’t gone in. Let’s think about an example.
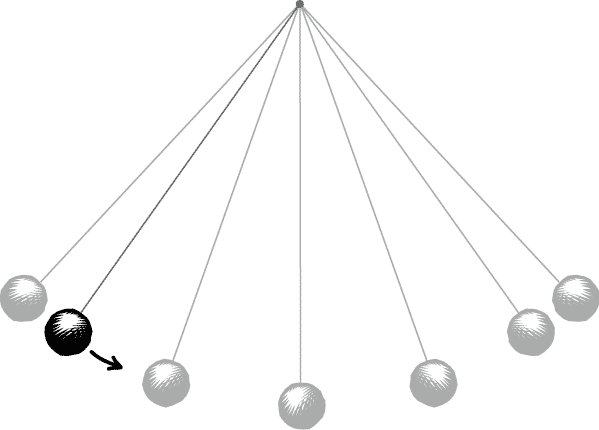
Picture a simple pendulum. Now imagine pulling the weight of this pendulum to either side so that if it were to be released it would start swinging back and forth. This is our initial state.
Now imagine letting go of this pendulum so that it does start swinging back and forth. This is our effect.
Suppose that the left-hand side of this pendulum suddenly became the right-hand side and that the right-hand side suddenly became the left-hand side – this is called a parity transformation.
If we think again about the effect of letting go of the pendulum we’ll see that it has changed: if the pendulum originally started swinging to the right then after this transformation it will instead be swinging to the left, and vice versa. This effect is not invariant under the parity transformation and so according to our definition it isn’t symmetrical.
If Curie’s principle is correct then the variance of our effect under a parity transformation will also be found in its cause; any effect should share the asymmetry of its cause. Luckily for Curie this is exactly what we find.
If we apply the parity transformation to our initial state we’ll find that the side to which we pulled the pendulum also changes from right to left. The asymmetry that we found in our effect is shared by its cause.
A simple failure?
This example may seem obvious. In fact, many people have thought that Curie’s principle itself is just obviously true. However, in ‘The Simple Failure of Curie’s Principle’ Bryan Roberts describes a way in which Curie’s principle fails.
Remember that Curie’s principle tells us that any symmetry or asymmetry present in an effect must have been present in its cause. So, in order for Curie’s Principle to fail we need to find a counter-example to this, we need to find a situation in which symmetry or asymmetry is not shared by cause and effect. We need to find a way of getting out what hasn’t gone in.
Roberts asks us to imagine a different symmetry transformation, one in which instead of swapping left for right it is the direction of time itself that is reversed. A nice way to picture this is to think about a film (this may come easier to those amongst us who can remember having to rewind VHS tapes!). If we imagine filming our pendulum swinging back and forth, the time reversal symmetry transformation will make our example look as if this film is being played backwards. When we play a film backwards, unlike in our parity transformation, everything remains in the same position in each individual frame and it is only the direction of movement that changes.
Now, let’s consider our example again. The initial state in which the weight is pulled to one side is going to look exactly the same after the time reversal. Why? Because there is not yet any direction of movement and, as we’ve seen, the weight’s position remains unaffected by time reversal. If this initial state remains unchanged then we can say that it is invariant under this symmetry transformation and so, going by our definition above, we can say that our initial state is symmetrical.
For Curie’s principle to fail for time reversal we need to find a later, asymmetric, state in our example that follows this symmetrical cause. As it turns out, these effects are very easy to find.
In our example the weight of the pendulum keeps swinging back and forth after it’s been released. At every point after its release, therefore, the weight has a direction of movement and so under time reversal this direction of movement will be reversed. If the weight has a direction of movement in these effects and this direction of movement is reversed by the time reversal then these effects are not invariant under this symmetry transformation and so aren’t symmetrical.
If our initial state was invariant under our symmetry transformation and all of these subsequent states are not invariant under this symmetry transformation then it looks as though we’ve found a way of getting out what hasn’t gone in after all.
Roberts has shown that, in the case of time reversal, Curie’s Principle fails. Simple.
By Ewan Rodgers
You can access a free preprint of ‘The Simple Failure of Curie’s Principle’ by Bryan W. Roberts. The article was published in Philosophy of Science. This work also led to the organisation of a symposium at the 2014 Meeting of the Philosophy of Science Association. Roberts has written a new paper following up on some different aspects of Curie’s principle, which is available on PhilSci-Archive.